Code

Summary

This is a python code to calculate Lindemann Index

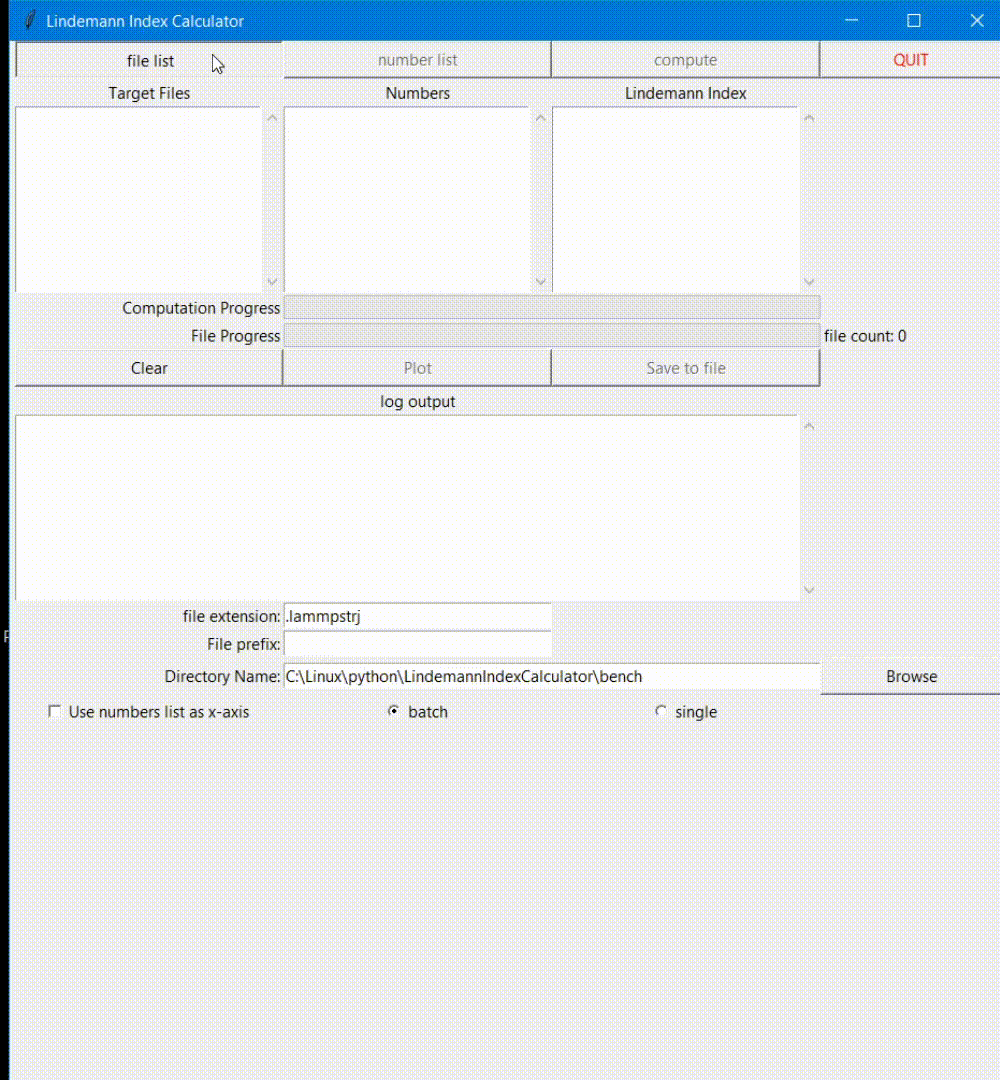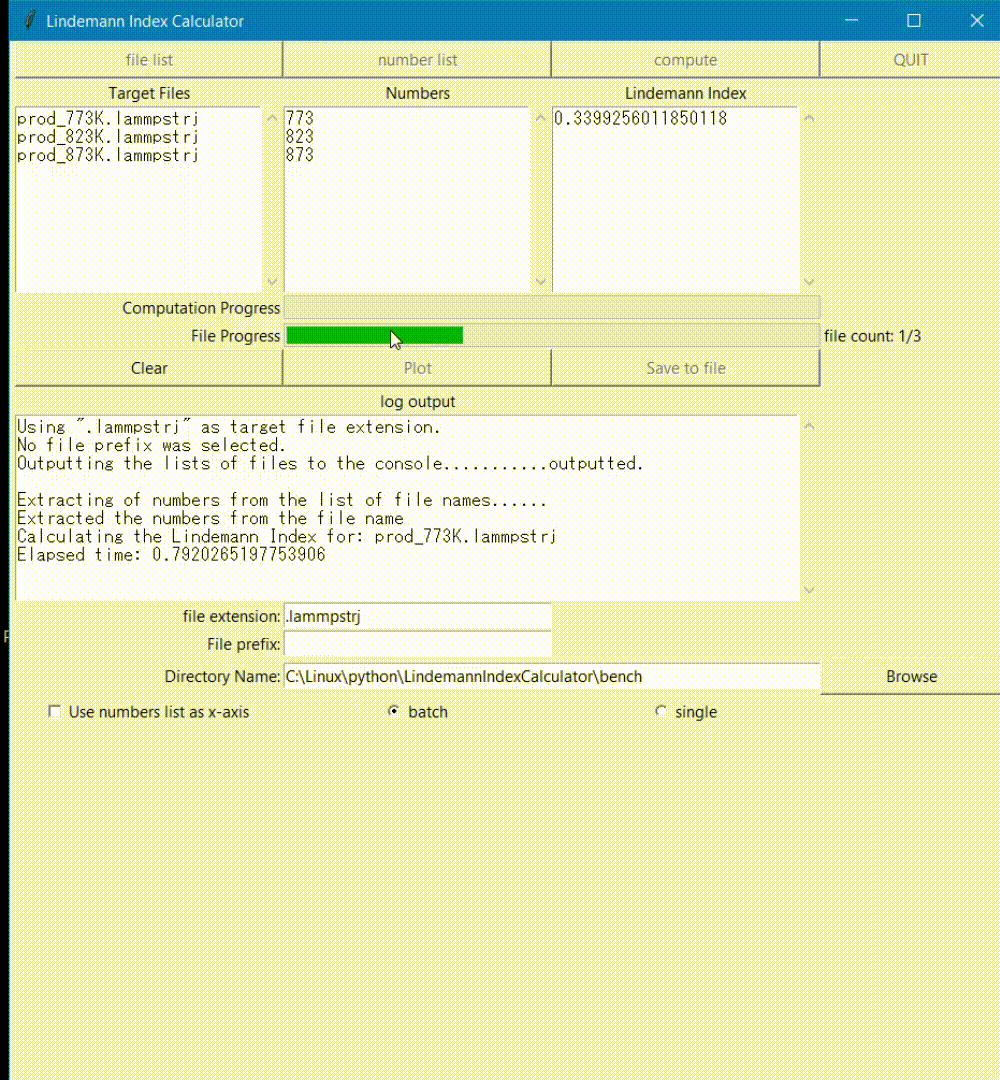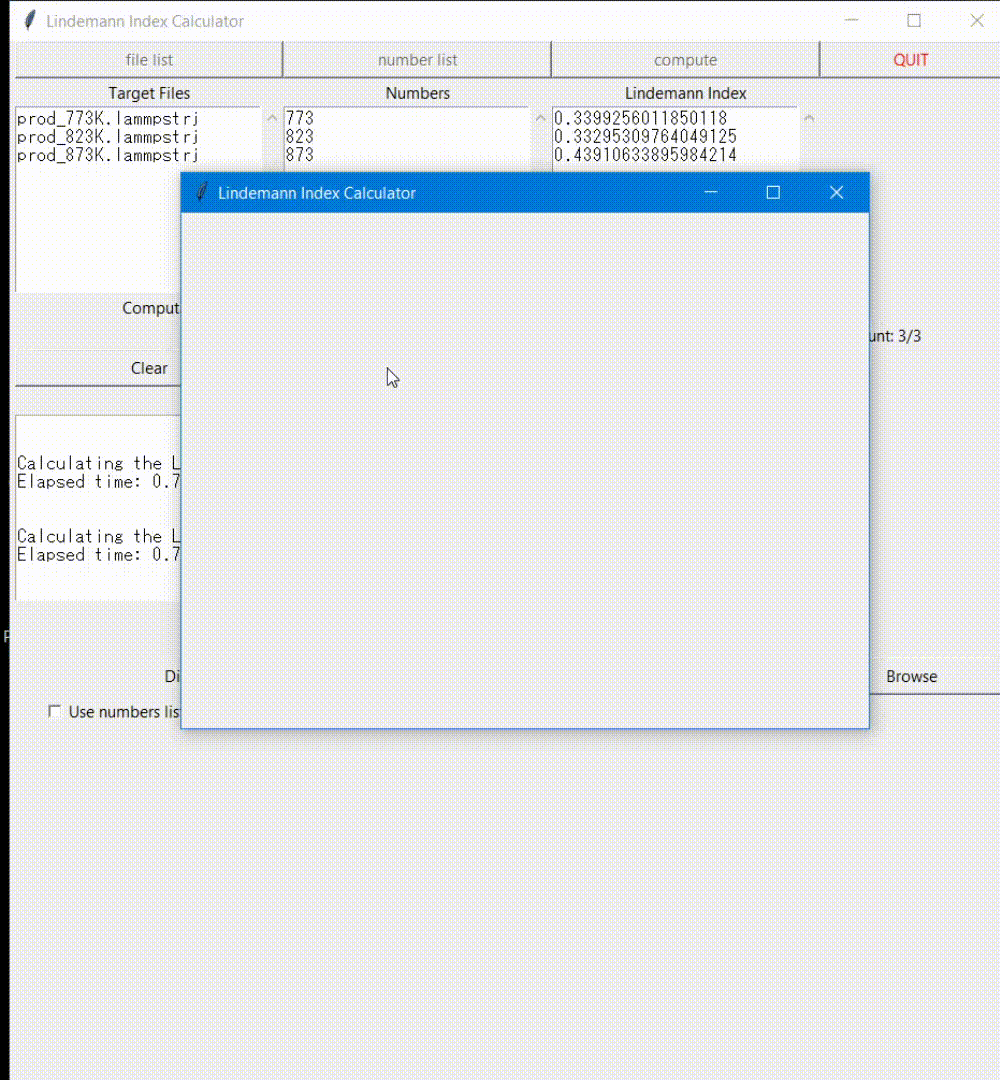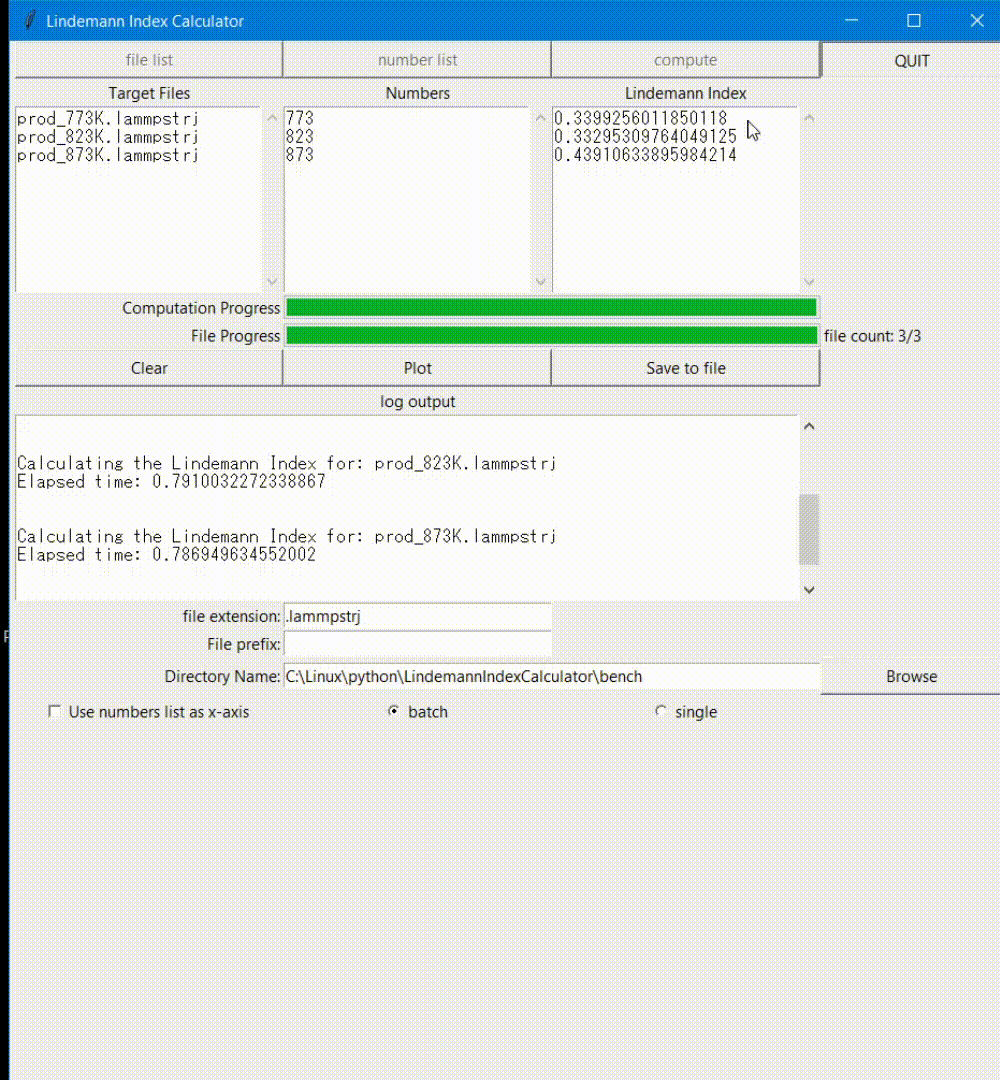
Motivation

I was working on my Molecular Dynamics Simulation and I had to calculate the Lindemann Index from the file. First, I tried to find a functionality in the visualization or post processing software, which turned out to be none. Then, I looked at other software and their features. Eventually realized that there is no Lindemann Index calculator, and since the formula was relatively simple, I ended up making a python script for it. And then I figured it would be cool to create a GUI for it so I tinkered with tkinter.

Theory

The Lindemann index is defined as the root-mean-square bond-length fluctuation with following mathematical expression:

\[\delta =\frac{2}{N(N-1)} \sum_{i \lt j}\sqrt{\frac{\langle r_{ij}^2 \rangle_t-\langle r_{ij}\rangle_t^2}{\langle r_{ij}\rangle_t}}\]

Where \(r_{ij}\) is the distance between atoms i and j , N is the total number of atoms, and the angle bracket \(\langle r_{ij}^2 \rangle_t\) represents that the distance is averaged over simulation time step, and \(\sum_{i \lt j}\) represents that summation of i<j. For example, if there is 3 atoms (Say, atom 1, atom 2, and atom 3), then the distance will be calculated between atom 1 & atom 2, atom 1 & atom 3, and atom 2 & atom 3.

Nutshell

Based on the formula, the brutal way of saying Lindemann Index is the mathematically accurate way of saying the dimensionless average distance among all the atoms. In fact, we are not interested in the value of the Lindemann index itself, rather interested in the change in Lindemann index. During the phase change (or say melting), the Lindemann Index will change by a factor of 3. This is because when the material is in a solid phase, the average distance between atom is relative small due to the crystal structure. However, when the material goes through phase change and become liquid, the atom will move around significantly more freely without a structure, increasing the average distance among them.

Why is Lindemann Index Useful?

Suppose you run a molecular dynamics simulation and attempt to melt some material. Based on the visual representation and dump file, you can somewhat tell if the object is melted or not. However, the result is rather conceptual and lack a concrete explanation. In order to account for it, the Lindemann Index is useful because it will quantatively represent the melting point of material in molecular dynamic simulation.

Requirement

• Please perform pip to install the dependencies

  pip install -r /path/to/requirement.txt
  

• Please prepare a dump file form lammps, preferably in .lammpstrj with dump style atom or .xyz with dump style xyz

Feature

• Batch computing
• Obtain atom coordinates using ovito pipeline
• Perform computation using numpy
• Vectorization to optimize the computation speed
• Progress bar for easy to understand progress
• File name extraction using regular expression to obtain temperature value form file name (proper set up for file name is recommended)
• GUI to simplify the use
• matplotlib integration for basic plotting
• saving the lindemann index into a txt file for future analysis
• Additional features will be implemented in the future

Citation

• F.A. Lindemann The Calculation of Molecular Vibration Frequencies.Phys. Z., 11:609,1910.
• A. Stukowski. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool.MODELLING AND SIMULATION IN MATERIALSSCIENCE AND ENGINEERING, 18(1), January 2010.
• S. Plimpton. Fast Parallel Algorithms for Short-Range Molecular Dynamics.Journalof Computational Physics, 117(1):1–19, March 1995.

Licensing

The project is licensed under MIT license